Quantization Error Propagation: Revisiting Layer-Wise Post-Training Quantization阅读笔记

motivation

现有量化方法多采用逐层量化的方法，然而量化误差会随着前向传播逐渐传递到更深的层。

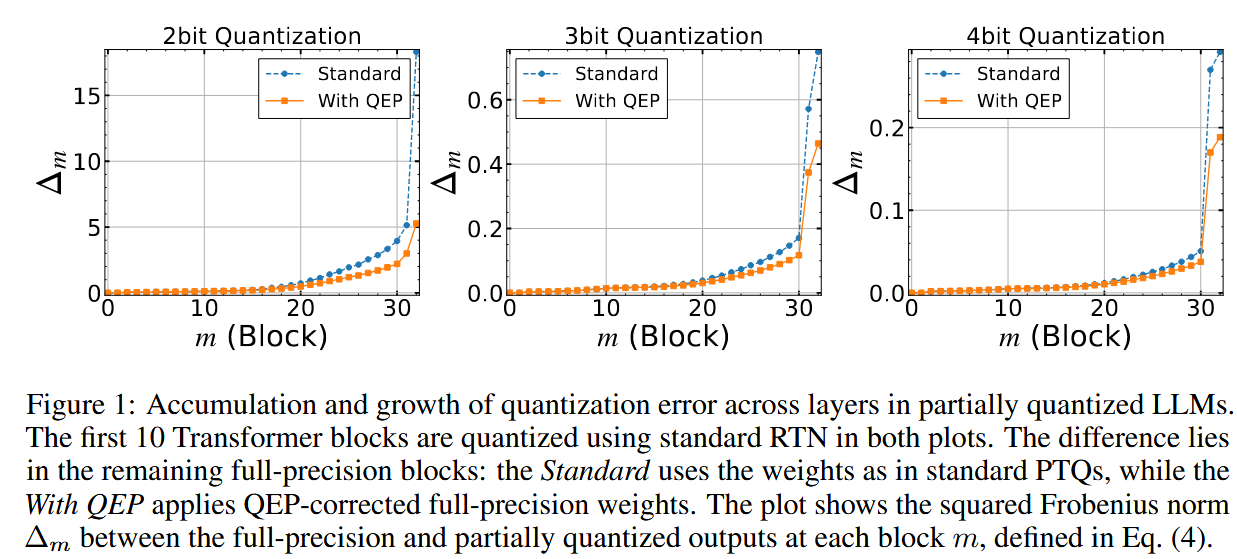
屏幕截图2025-04-16101008.png

尽管图中的层都是全精度的未量化，但可以看出量化误差仍随层深度呈指数型增长。

带代表量化了，否则表示全精度层。其中的纵轴量化误差表达式为：

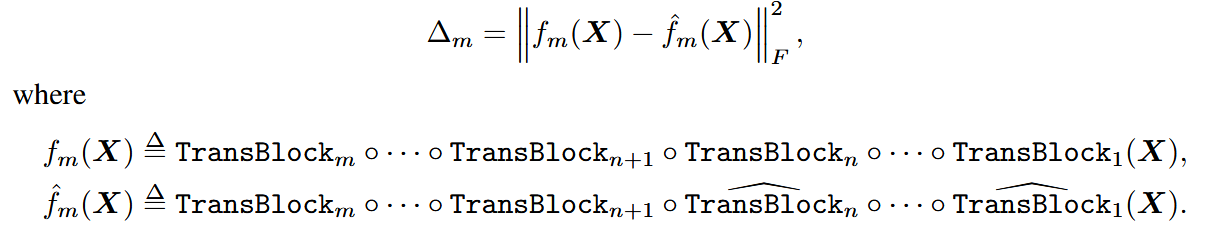
屏幕截图2025-04-16101333.png

创新点：考虑量化误差传播的量化方法

将量化目标重定义对齐每层在前层已经全量化前后的输出误差，形式化表示：

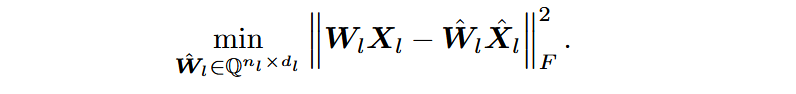
屏幕截图2025-04-16101528.png

记激活的量化误差为，则全精度输出可表示为，可得：

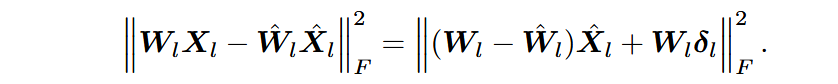
屏幕截图2025-04-16102135.png

为使其最小，当优化目标梯度为0时候，可得：

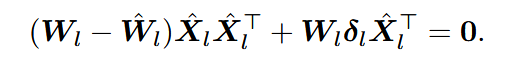
屏幕截图2025-04-16102238.png

引入经验Hessian矩阵，则上式可写作：

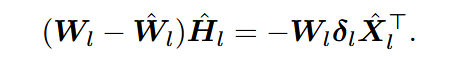
屏幕截图2025-04-16102447.png

当Hessian矩阵可逆时，均在右侧乘上，则可得最优量化后权重矩阵：

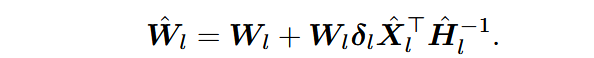
屏幕截图2025-04-16102554.png

然而，真实的经验Hessian矩阵可能是病态的或者是奇异矩阵，会造成数值稳定性上的问题，因此沿用GPTQ的damping策略，给矩阵对角线上的每个元素都加上原本对角线元素的绝对值，使其变成正定的可逆矩阵。

同时为了防止过拟合和过高的计算代价（计算经验Hessian矩阵），为原本的闭式解加上缩放系数变成：

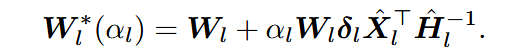
屏幕截图2025-04-16103200.png

主要还是针对MLP中一些维度比较大的层，直接将其设置成0退化为一般的量化方法可以大大节省计算开销并且避免过拟合问题。