Dobi-SVD

Dobi-SVD: Differentiable SVD for LLM Compression and Some New Perspectives阅读笔记

motivation

认为分解激活（这里的激活指的不是输入，是）比分解权重更好，提出了激活SVD分解后接无需LoRA的权重补偿新范式。同时提出了一种新的SVD分解矩阵储存方法使得分解秩与压缩率的关系变成一种双射，在保留更多信息的同时提高压缩率。

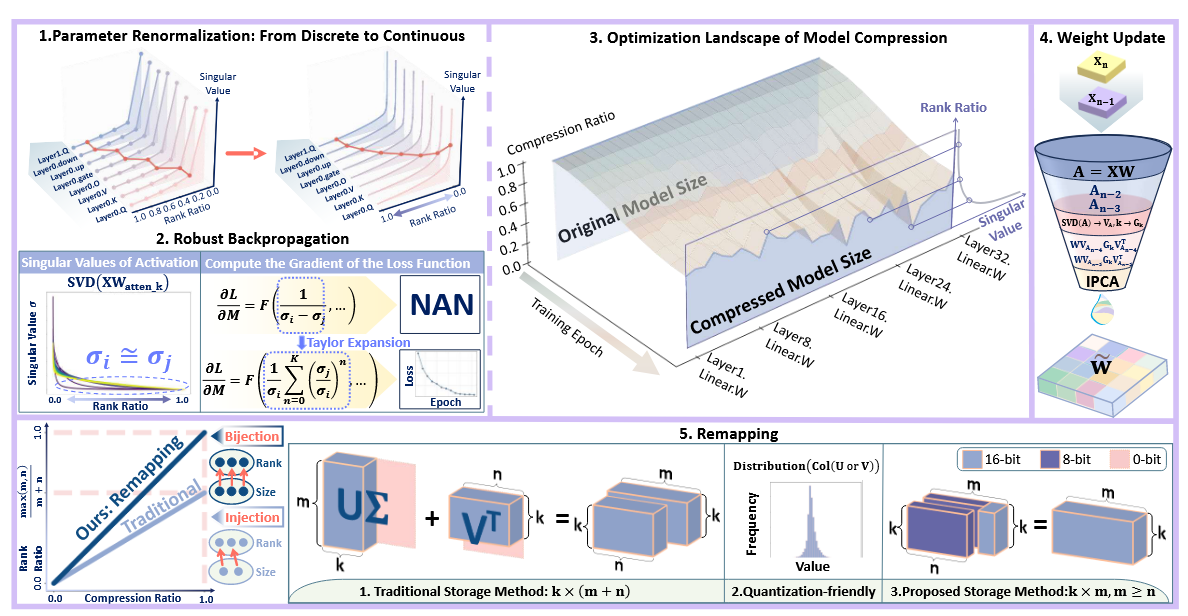
创新点1：逐层自动化目标秩判定

每个模型有L层，每一层有M层，假设每层对应的激活有n个奇异值，则可选择的截断（舍弃top k外的奇异值）位置有种，为了能自动化选取截断位置，需使截断函数可导，将奇异值改写为，其中是一个可学习参数，将其他参数冻结进行训练：

记SVD分解后的激活为，记关于用于提取反对称矩阵，则激活的梯度可表示为：

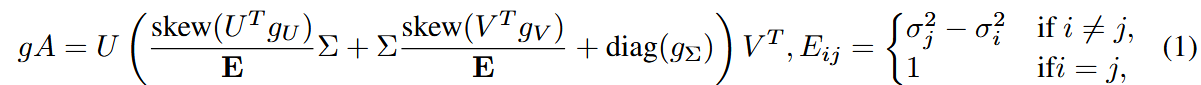
当相近时，会接近0，造成梯度爆炸。

为防止梯度爆炸，当且的时候，记

当相近但不接近0时，对其进行泰勒展开：

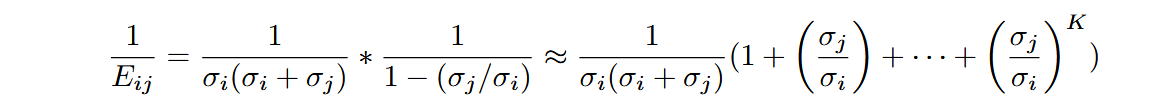
创新点2：权重更新补偿

设G为前k的对角元素为1，其他对角元素为0的矩阵，激活分解可看作：

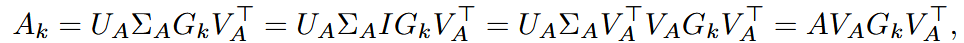
其中激活，则理想的更新后权重应满足：

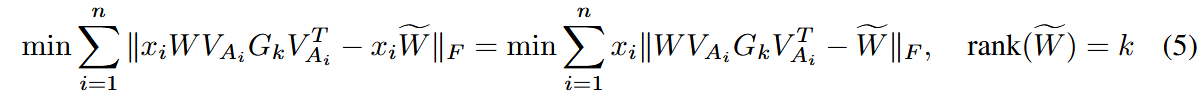
适用增量式主成分分析算法（IPCA）对其进行计算：

创新点3：混合精度矩阵存储

对于矩阵，传统方法压缩率为，k比矩阵秩小的时候压缩率就到1了，但这个时候矩阵信息还是有所损失的，感觉这里用单射来形容怪怪的。本文方法压缩率为

不妨令 ，对于更新后的权重进行SVD分解得到，提取的前列，形状为，其中前列采用8bit精度存储，提取的前行，也转换为 8bit，再和中 8bit 的那一堆一起存储即可。

其它

虽然都是在ICLR 2025上接受的，但这篇实际是在LLM-SVD的基础上进一步做的并和LLM-SVD进行了比较。