SVD-LLM: Truncation-aware Singular Value Decomposition for Large Language Model Compression阅读笔记

motivation

  • 当前基于奇异值分解的方法缺乏奇异值与量化损失函数之间具体的的关系证明，丢弃较小奇异值也可能导致较大的损失

  • SVD后没有对分解后的低秩向量微调补偿。

创新点1：分解前数据白化

首先收集校准数据，对进行Cholesky分解得到，取下三角矩阵作为白化矩阵，有：

记将奇异值分解为、、，其中

已知矩阵 A 的 Frobenius 范数（维度为 m×n）可以推导为它的 Gram 矩阵（）的迹的平方根。

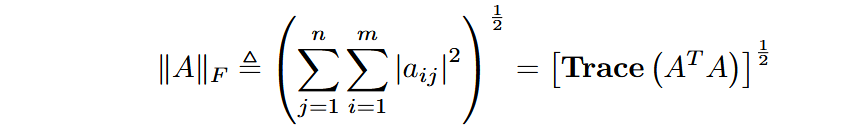
屏幕截图2025-04-11020501.png

截断一个奇异值时，其量化损失可表示为：

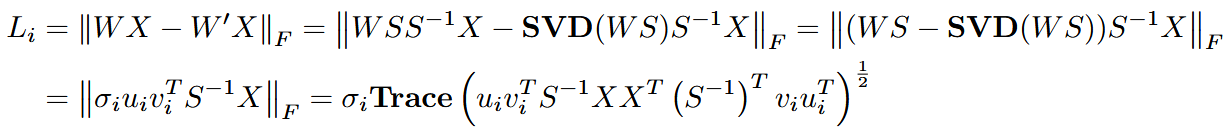
屏幕截图2025-04-11020700.png

带入，根据SVD分解性质，U、V间列向量均为单位正交向量，可证截断一个奇异值时其量化损失为奇异值大小：

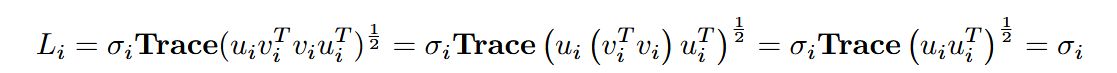
屏幕截图2025-04-11020920.png

同理，截断多个奇异值时，其量化损失为奇异值平方和的平方根：

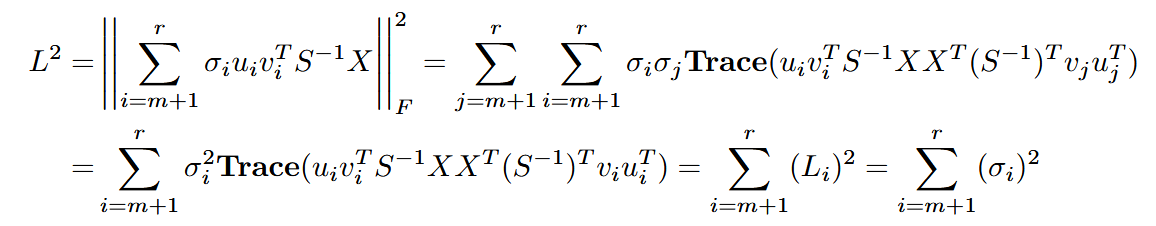
屏幕截图2025-04-11021446.png

创新点2：SVD分解后LoRA补偿

将权重矩阵分解为，因为两低秩分支在微调阶段的导数相互独立，、分别进行LoRA补偿：

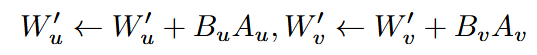
屏幕截图2025-04-11024538.png

其中、、、分别是和的LoRA参数，整体流程图：

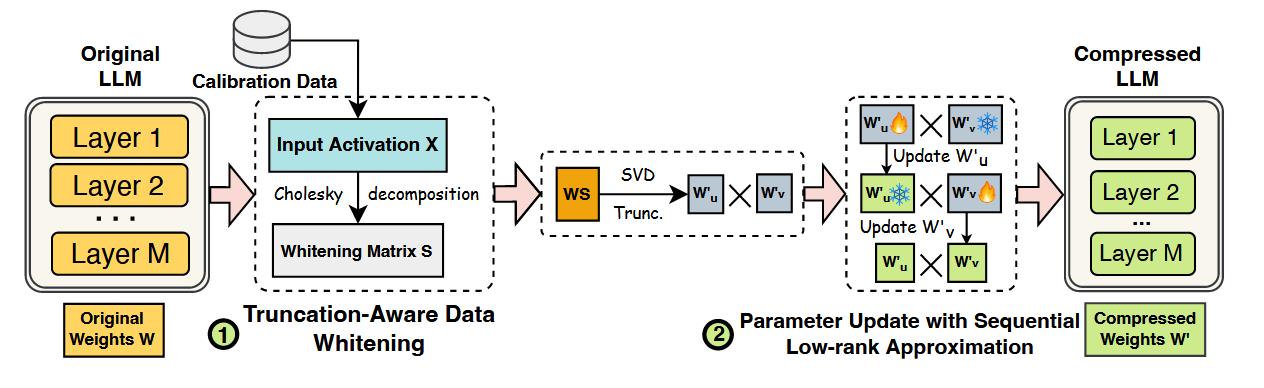
屏幕截图2025-04-11022210.png

其它

这个白化矩阵的应用倒是和CASP那篇基本一样，看了下时间似乎CASP晚些，但CASP主要聚焦于混合超低比特权重分解。