TEAL

Training-Free Activation Sparsity in Large Language Models阅读笔记

motivation

观察到LLaMA中各中间层的激活通常是零均值单峰分布的。且在MLP\注意力模块前的激活呈现高斯分布，内部激活呈现拉普拉斯分布，即，特征。大量在零点集中的激活启发了本文基于激活绝对值大小的激活稀疏方法。

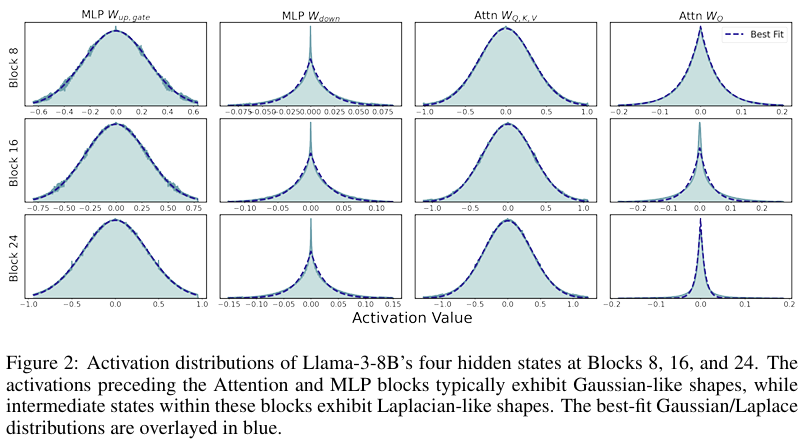
作者观察到权重通常为高斯分布，而当一个独立的各向同性高斯向量与一个独立的高斯矩阵相乘时，结果服从多变量广义拉普拉斯分布，之所以均值为零是由于正则化的影响，这可能能解释上述的激活分布。

背景

激活稀疏分为两大类：

第一种是input sparsity，即计算时，x中零元素对应的权重列不会被使用；

第二种是output sparsity，即计算时，s中零元素对应的权重行不会被用到

因此为了保证连续内存访问，对于input sparsity方法，权重要按列存储；对于output sparsity方法，权重要按行存储。

创新点1：基于激活绝对值的激活稀疏方法

尽管当权重矩阵对应通道的范数很大时，小激活也可以有大影响，但本方法很有效。

对于激活，和稀疏度，定义阈值：

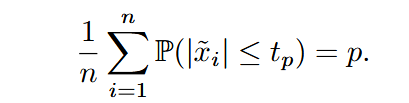
则稀疏化可表示为：

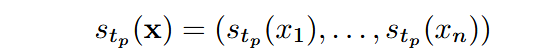
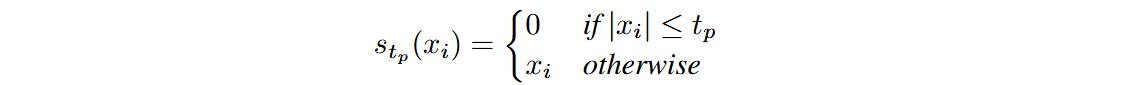
创新点2：逐块贪心优化策略

目标为在满足块稀疏目标的前提下，使得二阶范数损失最小。

取步长，每一轮尝试在各个层模拟完成使得总模型稀疏度增长的操作，遍历后选择二阶范数损失最小的一个进行真正的操作。这里似乎不太对，好奇看了眼代码似乎default是0.9，如果是1的化相当于所有激活都变零了。

其它

此外还实现了硬件加速，按列存储权重矩阵，根据激活掩码选择性加载权重列，使用了SplitK 工作分解。