KurTail

发表于2025-03-12|更新于2025-03-12

|浏览量:

KurTail : Kurtosis-based LLM Quantization阅读笔记

motivation

对于使用旋转矩阵来抚平outlier的方法，随机旋转矩阵不够优，端到端loss训练的学习旋转矩阵又太费计算资源，于是提出了一种聚焦于tail density（通常指的是概率分布尾部的概率密度，即随机变量取值在远离分布中心的区域的概率密度，它反映了分布尾部的“厚重”程度）的旋转矩阵学习方法。

背景补充

峰度

表征概率密度分布曲线在平均值处峰值高低的特征数，直观看来，峰度反映了峰部的尖度。
计算公式：
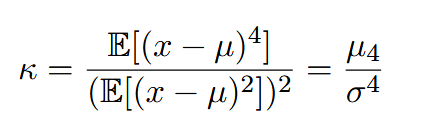
正态分布峰度为3，大于3为正峰度，代表数据中有更多的极端值。

主要创新点：基于峰度的旋转矩阵学习方法

基于峰度的损失函数：

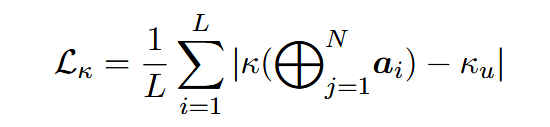
屏幕截图2025-03-12022530.png

其中，代表将第层所有激活进行拼接。

采用逐层优化策略，首先运行原始模型并存储MHSA和FFN块的输入，然后创建一个只有一个线性层的小模型来模拟量化前的输入，最后使用Kurtosis损失函数训练旋转。为了进一步优化，在训练时将不同层的输入混在一起。
为了在不量化的时候模型输出不变，旋转矩阵的学习需要在正交空间内进行优化，使用Caley Adam优化器来强制约束。

文章作者: Wotoosh

文章链接: https://wotoosh.github.io/2025/03/12/KurTail/

版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源由本自性清净故，令诸爱染悉无垢！

相关推荐

BCQ: Block Clustered Quantization for 4-bit (W4A4) LLM Inference阅读笔记创新点1：将向量聚块量化对于一个有元素的向量，将连续个元素分为一个块，用个密码本进行量化整个量化过程分为两步：第一步为每个块分配一个密码本用于量化，第二步在相应密码本里寻找每个元素用于量化的条目。每个块可视为一个array，共享一个缩放参数，每个向量有一个缩放参数，将量化到位。最终该方法占用的实际位宽为：创新点2：局部最优块聚类量化算法最初利用Kmeans++算法初始化密码本中的元素，固定密码本，根据MSE寻找每个块的最优密码本，即：再固定密码本选择策略，利用LloydMax算法为每个密码本寻找最优元素，反复迭代直至收敛或达到指定次数。

BoA: Attention-aware Post-training Quantization without Backpropagation阅读笔记motivation基于梯度的重建优化方法受参数规模限制难以迁移到大语言模型上，传统的基于变换的量化方法又欠考虑了层间关系，因此提出了一种无需BP，综合考虑QKVO层相互依赖的量化方法。创新点1：基于QKVO层相互依赖的重建优化方法本方法于GPTQ类似，在量化后对其余未量化权重进行更新以补偿量化损失，更新公式：其中H是Hessian矩阵，Chol(·)代表Cholesky分解，因此U是上三角矩阵且为了弥补GPTQ的Hessian估计方法只与输入有关，与注意力模块其他层无关的问题，本方法提出了新的Hessian估计方法：推导主要利用了对于的二阶导是，其中J为关于softmax函数的Jacobian矩阵。创新点2：高效实现relaxed...

CBQ: Cross-Block Quantization for Large Language...

FlexRound: Learnable Rounding based on Element-wise Division for Post-Training Quantization阅读笔记核心创新点：基于逐元素触发的灵活舍入提出一种新的权重舍入机制，S为与W相同形状的scale矩阵，其中的每个元素都是正且可学习的，其中的和都是通过最小化学习到的。由于层不同通道输出差异大，在实际应用时，对线性层还需引入；对2D卷积需引入和，最终量化公式：其它暂时还没想明白每个权重都配了一个scale辅助量化，量化后使用的内存不是更大了吗，有机会再研究一下。

LRQ: Optimizing Post-Training Quantization for Large Language Models by Learning Low-Rank Weight-Scaling Matrices阅读笔记motivation 仅权重量化只在小batch推理时加速才明显，权重激活量化则精度下降太多。众多方法中SmoothQuant和FlexRound都使用了硬件有好的per-tensor静态量化，但前者精度下降过高，后者因为要学习过多参数泛化性能不够好（MMLU上表现不够理想）。创新点：权重矩阵低秩分解权重分解核心公式：其中，、相乘后得到与权重维度的矩阵，、，为行/列向量，收低秩矩阵在推荐系统中的应用启发。最终目标为最小化块量化损失

LeanQuant: Accurate and Scalable Large Language Model Quantization with Loss-error-aware Grid阅读笔记motivation 认为传统的min-max对称网格量化无法很好地处理Hessian逆矩阵中的outlier。基于OBQ思想，认为量化损失与权重量化误差的平方、逆Hessian矩阵对角的元素的倒数成正比创新点：Loss-Error-Aware-Grid 核心思想：用逆Hessian矩阵对角的元素的倒数为量化误差加权。非均匀网格优化目标：均匀间隔网格初始化，再通过kmeans进行学习均匀网格优化目标：其中 R=max(w)-min(w)，T是控制搜索粒度的超参数。其它主要延续了GPTQ的思想，在GPTQ基础上做了网格量化。 document.addEventListener("DOMContentLoaded", function() { renderMathInElement(document.body, { ...