Identifying Sensitive Weights via Post-quantization Integral阅读笔记

对于现有的敏感度指标的分析

现有的敏感度指标主要基于梯度与Hessian矩阵（使用Fisher准则估计）

  • 由于模型量化后的权重可能超出收敛半径，导致泰勒展开近似失效，传统的Hessian矩阵估计也不准。
  • 层与层间互相不独立，单独计算每层的权重敏感度变得不可靠。

创新点1： 后量化积分（PQI）

通过积分路径上的梯度信息，能够更准确地估计量化对损失函数的影响，即将量化损失计算改写为

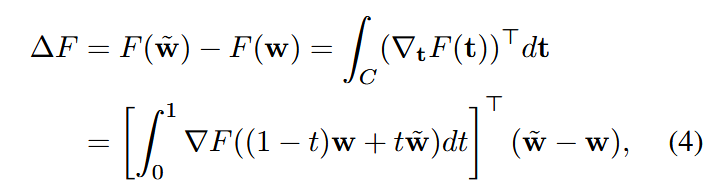
屏幕截图2025-03-08205912.png

其中C是从到的任意路径，PQI可定义为

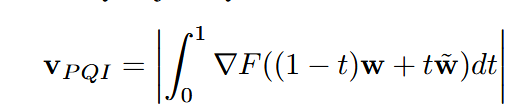
屏幕截图2025-03-08210044.png

量化损失差改写为

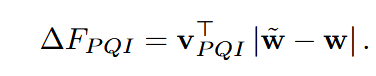
屏幕截图2025-03-08210215.png

其中代表取每个元素的绝对值，防止正负梯度项相互抵消，以提高泛化性。

在实际使用时，使用矩形估计的方法：

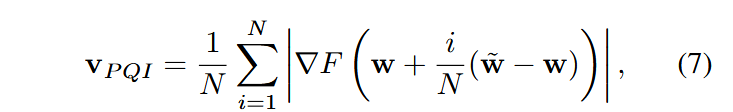
屏幕截图2025-03-08210759.png

由于F的增长与成线性，因此解决了层间不独立的问题；由于PQI将路径分成很多小段，使得每段都落在收敛范围内，因此使得其估计值保持准确。

观察到较浅的层往往有较大的，且一层中的不同projection layer也有不同的敏感性。

创新点2：ReQuant框架

中心思想：将矩阵分解为低精度量化矩阵与高精度异常值()和高精度重要权重()的和。

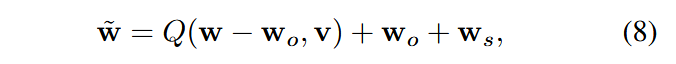
屏幕截图2025-03-08211630.png

自适应异常值选择

中心思想：为具有更大的的层分配更多的异常值额度

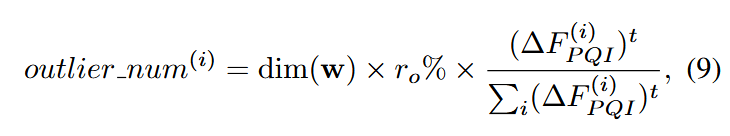
屏幕截图2025-03-08211930.png

其中是全局异常值比率，t是温度系数，对于不同温度进行网格搜索，选取绝对值最大的相应数量的权重作为异常值，选取最小量化误差的组合。

分步重要权重分离

中心思想：根据使用贪心策略分多次选出的重要权重用高精度存储。